Memang benar bahwa setiap kali David Beckham bersiap menendang bola, dia selalu memperhitungkan spin bola yang tepat, kecepatan dan mengambil sudut tembak yang diperlukan sehingga selalu mampu memperdaya lawan.
Efek Magnus
Pada saat bola ditendang dan melayang di udara dengan spin/putaran bola, maka selama melawan aliran udara, menurut prinsip Bernoulli pada kedua sisi bola terjadi tekanan yang berbeda. Perbedaan tekanan ini menghasilkan gaya yang dikenal sebagai efek Magnus, atau kadang dikenal juga sebagai gaya angkat/lift (lihat gambar 1).
Arah spin
Arah aliran udara Arah bola
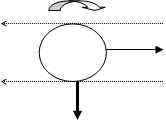 Gaya dari efek Magnus
Gaya dari efek Magnus
Gambar 1
Besar gaya dari efek Magnus yaitu :
FL = CLrD3fv
Dimana CL adalah koefisien lift, r adalah kerapatan udara, D adalah diameter bola, f adalah frekuensi spin bola, dan v adalah kecepatan bola.
Bagaimana Beckham membelokkan (swing) bola
Beckham terkenal sebagai ahli membuat ‘tendangan pisang’ (swing) bola. Kemahiran itu secara fisika dapat diperhitungkan dengan tepat dan akurat. Dapat diandaikan bahwa suatu tendangan bebas misalnya berjarak 25 m dari gawang, dan bola ditendang dengan kecepatan 25 m/s, dalam hal ini menyebabkan spin bola pada frekuensi 10 putaran/s. Dengan mengandaikan kerapatan udara 1,2 kg/m3 dan diameter bola menurut ketentuan FIFA 0,22 m, dengan mengasumsi koefisien lift sebesar 1,23 maka gaya angkat (lift) atau gaya magnus dapat dihitung sebagai berikut.
FL = CLrD3fv
= 1,23 x 1,2 x 0,223 x 10 x 25
= 3,93 N
Percepatan bola dapat dihitung dari rumus F = m.a.
Standar massa bola oleh FIFA antara 0,410 kg – 0,450 kg atau dirata-rata 0,430 kg.
F = m.a a = F/m = 3,93 / 0,430 = 9,14 m/s2
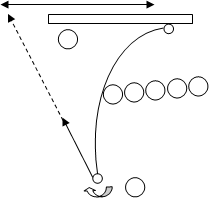
Waktu terbang bola diperkirakan 1 detik maka kurva belokan (swing) bola dapat dihitung sebagai berikut (lihat gambar 2).
s = vo.t + ½ at2
= 0 + ½ x 9,14 x 12
= 4,57 m
Penjaga
gawang
lintasan bola
dinding pertahanan lawan
v = 25 m/s
posisi awal bola
Beckham
arah spin bola
Gambar 2
Pada contoh perhitungan di atas gaya gesekan diabaikan. Namun kalangan pelajarpun tahu bahwa gaya gesekan itu ada. Gaya gesekan selalu bekerja melawan arah gerak bola, yang akan memperlambat dan menurunkan bola. Rumus untuk menghitung gaya gesek pada bola selama melayang di udara adalah sebagai berikut.
Fd = ½ CdrAv2
Dimana Cd adalah koefisien gesek, r adalah kerapatan udara, A adalah luas penampang permukaan bola (jika diameter D = 0,22 m maka A = ¼ p D2), dan v adalah kecepatan bola.
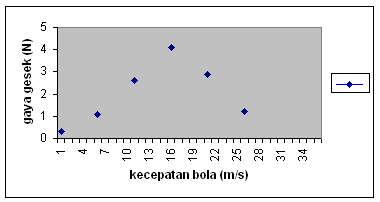 |
Besar koefisien gesek relatif tidak konstan. Untuk udara yang sejuk justru kecepatan bola sangat mempengaruhi koefisien gesek yang pada akhirnya mempengaruhi besar gaya gesek. Variasi besar gaya gesek dengan perubahan kecepatan bola dapat ditunjukkan pada grafik berikut ini.
Jadi bila pemain menendang bola cukup keras dengan kecepatan 25 m/s – 30 m/s tidak hanya bola melaju dengan cepat tetapi bola juga akan mempertahankan kecepatan yang dimilikinya lebih lama dibanding bola lambat.
Bagaimana Beckham menendang bola begitu keras
Dalam peristiwa tumbukan antara kaki dengan bola diperoleh bahwa kecepatan bola tergantung pada massa kaki pemain, dan massa bola serta koefisien restitusi. Rumus untuk menentukan kecepatan bola adalah sebagai berikut.
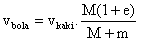
Dimana v adalah kecepatan, M adalah massa kaki, m adalah massa bola, e adalah koefisien restitusi dengan perkiraan realistis e = 0,5.
Jika 1 + e = 1,5 dan M/M+m =0,8 maka bentuk sederhana dari kecepatan bola adalah :
vbola = 1,2 vkaki
Hal inilah yang akan diperhitungkan Beckham untuk menendang dengan kecepatan kaki 20,8 m/s agar mendapatkan kecepatan bola 25 m/s.
Gerak peluru
Selain dengan tendangan
pisang (swing) untuk melewati tembok pemain lawan, terkadang pemain
harus menendang dengan ‘mencungkil’ bola untuk melewati tembok pemain,
dengan lintasan parabola. Beberapa persamaan gerak peluru berikut ini dapat diterapkan untuk kondisi itu.
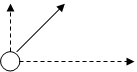
Y vo
Jarak mendatar : X = vot cosq
Ketinggian : Y = vot sinq – ½ gt2
Waktu terbang bola : t = (2 vo sinq)/g
Jarak tembak maksimum : Xm = (vo sin2q)/g
Ketinggian maksimum : Ym = (vo2 sin2q)/2g
Dengan asumsi jika waktu t = 0 maka X dan Y sama dengan nol.
Perhitungan yang sering dilakukan yaitu
dengan mengabaikan gaya gesekan udara. Setelah mengetahui pentingnya
faktor gesekan ini maka bagaimana menempatkan gaya gesekan ke dalam
setiap perhitungan (lihat gambar 3).
Bola, seperti halnya peluru selama geraknya dikenai tiga gaya, gaya beratnya mg, gaya Magnus jika berpusing/spin sebesar CLrD3fv, dan gaya gesek sebesar ½ CdrAv2.
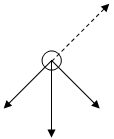 Vektor kecepatan
Vektor kecepatan
CLrD3fv
½ CdrAv2.
mg
Gambar 3
Resultan vektor gaya akan memberikan arah bola, dan besarnya dapat dihitung, misalnya dari :
Fresultan = m.a dan w = m.g
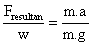
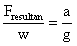
Akhirnya dapat disimpulkan bahwa alternatif pendekatan pengajaran fisika dengan menggunakan variasi topik-topik fisika akan dapat membawa para pelajar lebih tertarik (interest). Murid-murid yang tertantang diharapkan dapat menggali sendiri lebih jauh topik keseharian pada olah raga atau bidang lain, menurut konsep-konsep fisika.
Tidak ada komentar:
Posting Komentar